Study Guide
Field 121–124: Upper Elementary (3–6) Education
Subtest 3: Mathematics
Sample Multiple-Choice Questions
Expand All Answers | Collapse All Answers
Subarea 1—Mathematics-Specific Teaching Practices
Objective 001—Build and draw on relationships with children, caregivers, and communities in ways that support all children's mathematics learning.
1. A sixth-grade teacher prepares for parent-teacher conferences. Based on data from a recent survey, the teacher is aware that many parents/guardians have questions about supporting their children's mathematical understanding outside of school. Which of the following resources is most effective for promoting parents'/guardians' ability to support their child?
- workshop demonstrations and tutorial videos that explain relevant mathematics concepts and models
- a summary of assessment data illustrating students' progress in mathematics
- a list of online resources for mathematics definitions and articles
- printed copies of student learning standards for mathematics
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
- Correct. These resources empower parents/guardians to understand the relevant mathematics and provide their children with effective learning support.
- This summary focuses on students’ performance, which provides very limited information for parents/guardians to use to support their child.
- This information may prove useful in specific instances, but it does not encourage parents/guardians to connect with the relevant mathematical concepts that their child is learning.
- This information does not provide parents/guardians with strategies that they can use to support their child's mathematical learning.
Objective 002—Plan mathematics lessons and sequences of lessons.
2. A third-grade teacher finds this activity about area and perimeter online:
- Give each student twelve 1-inch squares.
- Tell the students to arrange the squares so that they make a shape with no gaps or overlaps.
- Ask the students to count the tiling to determine the area and count the side lengths to determine the perimeter.
- Have students compare their observations about the shapes and measurements with a classmate.
Which of the following learning goals aligns to this activity?
- Determine that two shapes can have the same area but different perimeters.
- Solve real-world problems involving the area and perimeter of several polygons.
- Divide shapes into equal areas and express each part as a unit fraction of the whole.
- Represent the distributive property using area models with whole-number side lengths.
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
- Correct. Different configurations of the tiles result in shapes that must always have the same area but can have different perimeters.
- The square tiles limit the scope of the activity to rectilinear area, so it would be difficult to model and solve problems involving various polygons such as triangles, pentagons, etc.
- The activity focuses on how perimeter can vary in shapes with the same area, which is not well-aligned to an investigation of unit fractions as described in this response.
- Representations with the distributive property would require the squares to be arranged into arrays, but the activity encourages students to create compositions that may differ from this configuration.
Objective 003—Use formative and summative mathematics assessments to gauge children's learning and to make instructional decisions.
3. A teacher has students complete this task before instruction on comparing fractions with unlike denominators.
| Use the less than sign, the greater than sign, or the equal sign to complete the comparison.
1 fifth a blank square meant to provide space for a student to write in an equal sign, a less than symbol, or a greater than symbol 1 tenth |
Using words and drawings, explain why you chose your answer.
|
|
Use the less than sign, the greater than sign, or the equal sign to complete the comparison.
1 third a blank square meant to provide space for a student to write in an equal sign, a less than symbol, or a greater than symbol 2 sixths |
Using words and drawings, explain why you chose your answer.
|
| Use the less than sign, the greater than sign, or the equal sign to complete the comparison.
3 eighths a blank square meant to provide space for a student to write in an equal sign, a less than symbol, or a greater than symbol 4 sevenths |
Using words and drawings, explain why you chose your answer.
|
This type of pre-assessment supports instruction primarily by allowing the teacher to:
- support students' ability to express mathematical understanding using symbols and representations.
- support reflective practice by collecting classroom artifacts to discuss with other teachers.
- determine which mathematics concepts require additional assessment.
- determine students' level of understanding of a mathematics concept.
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
- This task allows students to use symbols and justify their decision, but it does not provide students with the information necessary to support their correct use of the symbols.
- The primary goal of any assessment should not be to collect artifacts for reflection.
- The primary goal of this type of pre-assessment is to help the teacher establish students’ baseline levels of understanding before they receive instruction, not to identify specific skills that require additional testing.
- Correct. The pre-assessment allows the teacher to establish students’ baseline levels of understanding about the inequality symbols and the concept of fraction comparison before they receive instruction.
Objective 004—Enact instruction that allows all children to engage with significant mathematics and to develop productive dispositions toward mathematics.
4. Which of the following teacher practices best facilitates students' productive struggle during complex mathematical tasks?
- planning tasks that support a foundation for reasoning
- praising students for the amount of time they spend on task
- allowing students extra time to process mathematics questions
- providing nonroutine problems that support student-centered solutions
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
- Tasks that focus on reasoning (e.g., deduction, inference, sense-making) do not necessarily foster habits associated with productive struggle (e.g., perseverance, flexible thinking, curiosity).
- Encouraging students to spend significant time on a task does not necessarily encourage them to learn strategies to engage in productive struggle.
- Providing extra time does not inherently support students’ engagement with productive struggle.
- Correct. Nonroutine problems with student-centered solutions support productive struggle by promoting creative risk-taking, flexible thinking, and perseverance.
Subarea 2—Mathematical Knowledge for Teaching Grades 3–6: Whole Numbers and Operations
Objective 005—Unpack mathematical content and identify mathematical competence for whole numbers and operations.
5. Elementary students work on a series of addition problems.
185 plus 16 = blank space meant to provide space for a student to write their answer
185 plus 17 = blank space meant to provide space for a student to write their answer
185 plus 18 = blank space meant to provide space for a student to write their answer
This activity creates mathematical affordances for which of the following skills?
- using readily recognizable patterns to solve equations
- using the standard addition algorithm to calculate sums
- using place value to round to the nearest whole number
- using the associative property to establish relationships between addends
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
- Correct. This activity allows students to recognize and apply the fact that increasing one addend by 1 increases the entire sum by 1.
- The progression of problems is intentionally designed to promote pattern recognition without the use of the standard algorithm.
- The activity involves addends and sums that are all whole numbers, so rounding to the nearest whole number is not necessary in this context.
- Each problem involves only two addends, so the use of the associative property is not effectively supported by this task.
Objective 006—Perform mathematical explanations and support children's mathematical explanations for whole numbers and operations.
6. A student tells the teacher, "Look! I figured out a new way to do multiplication. I never need to multiply by two digits again! It just takes a few steps." The student demonstrates on the board:
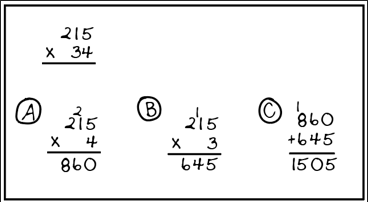
The expression 215 times 34 appears at the top of a student work sample. Three additional computations appear beneath it. The first computation, marked A, shows 215 times 4 equals 860. The second computation, marked B, shows 215 times 3 equals 645. The third computation, marked C, shows 860 plus 645 equals 1505.
Which of the following teacher responses would best help the student improve the accuracy of their method?
- "Is the 3 equal to 3 or 30?"
- "Is this three-step model like multiplying using expanded form?"
- "Would your method also work if you reversed the digits and multiplied 512 and 43?"
- "If you multiply 34 by 2, 1, and 5 and then added those products, would you get a different answer?"
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
- Correct. This response guides the student to identify their specific misconception about place value, which allows for the student to make improvements to their strategy.
- This response does not effectively guide the student to improve the solution strategy by addressing their place-value misconception.
- Changing the factors in this way does not effectively guide the student to improve the solution strategy by addressing their place-value misconception.
- The student is unlikely to improve their solution strategy until they observe that the answer to their original problem is incorrect.
Objective 007—Choose, interpret, and talk with representations for whole numbers and operations.
7. A third-grade teacher provides each student with a set of 24 counters and asks the students to make as many different groups of equal size as they can from the counters.
Student A: I split them in half and made 2 piles of 12.
Student B: I counted by twos and made 12 groups of 2.
Student C: I split them in half, then half again to get 4 piles of 6.
Which of the following questions can the teacher ask to foster students' understanding of the relationship between groups of equal size, addition, and multiplication?
- "Why do each of your piles have an even number of counters?"
- "Are the counters easier to count when they are sorted into piles?"
- "Can you explain why breaking the counters into groups is helpful?"
- "Why can we skip-count your different piles and get the same number?"
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
- This question may suggest that all factors of 24 are even, but it is possible for a pile to contain an odd number of counters (i.e., 8 times 3).
- This question does not guide the students to make connections about groups of equal size, addition, and multiplication.
- This question could lead students to describe groupings of the counters that are based on place-value (i.e., 10 plus 10 plus 4), rather than connecting equally sized groups with addition and multiplication.
- Correct. To respond to this question, students must consider the relationships between addition and counting, multiplication and repeated addition, and how the size of the groups connects to skip-counting.
Objective 008—Elicit, interpret, support, and extend others' mathematical thinking for whole numbers and operations.
8. Third-grade students solve subtraction problems that require regrouping. A student describes the strategies they used to solve 76 – 28: "I started with 28 and skip-counted on by tens. So, 38, 48, 58, 68. 68 is almost 70, so I counted on by 2 to get to 70. Then 6 more to 76. I added up the tens and the 2 and the 6 to get 48. That's the answer." The teacher models the explanation for the class on the board, as shown.
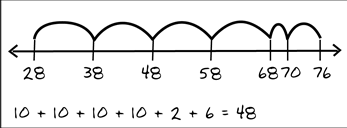
A marked-up number line and addition work are shown. The number line includes tick marks that are labeled 28, 38, 48, 58, 68, 70, and 76. Arcs connect these tick marks above the number line. Below the number line is the sum 10 plus 10 plus 10 plus 10 plus 2 plus 6 equals 48.
The teacher's action best extends students' thinking primarily by:
- fostering their mathematical confidence.
- constructing models to demonstrate mathematical explanations.
- encouraging them to select efficient models to solve given problems.
- providing alternative strategies for checking their own work for accuracy.
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
- Any increase in mathematical confidence developed from using a model follows as a result of its primary purpose: to represent knowledge in a way that promotes student understanding.
- Correct. The teacher extends the students’ thinking by providing them with an additional model that they can use to solve other problems and interpret explanations.
- The students did not have to select any models for this task.
- The teacher faithfully records the student’s solution without providing any alternative strategies.
Subarea 3—Mathematical Knowledge for Teaching Grades 3–6: Fractions, Decimals, and Operations
Objective 009—Unpack mathematical content and identify mathematical competence for fractions, decimals, and operations.
9. A fifth-grade student compares the value of 1 fourth and 1 third. The student shares this conclusion.
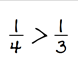
The inequality one-fourth is greater than one-third is shown as part of a student's work.
Which of the following responses by the teacher would best reveal the student's understanding about comparing fractions?
- "Let's try using these fractions in a word problem."
- "Let's try interpreting these fractions with place value."
- "Can you represent these fractions on a number line?"
- "Can you rewrite these fractions with a common denominator?"
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
- This response does not encourage the student to explain how they compared the fractions.
- The denominators of these fractions are not written in a power of 10.
- Correct. This question encourages the student to demonstrate how they interpret each fraction and apply number sense and comparison skills to position the numbers on the number line.
- This question guides the students to a method of comparing fractions—rewriting each with a common denominator and then comparing their values—rather than encouraging the student to reveal their thought processes directly.
Objective 010—Perform mathematical explanations and support children's mathematical explanations for fractions, decimals, and operations.
10. Fifth-grade students practice addition of decimals to hundredths by solving money problems. Some students in the class demonstrate mastery of this skill. Which of the following activities would be most appropriate for helping these students build on and expand their understanding of decimal addition?
- practicing ordering with tenths, hundredths, and thousandths
- solving money problems that involve adding mixed numbers with tenths and hundredths
- using the same addition strategies to add metric measurements with decimals to hundredths
- explaining how they can convert sums of money and other numbers with tenths and hundredths into fractions
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
- The skills of addition are typically taught after the skills of ordering decimal values, so this activity would likely be a review for the students who have practiced adding decimals.
- Using mixed numbers to describe an amount of money is inconsistent with the way that money is described outside of the classroom.
- Correct. This activity expands student understanding of decimal addition by broadening the application of their skills to include contexts that are not limited to money.
- This activity doesn’t build on the task of adding decimals, and including it shifts the focus away from that learning goal.
Objective 011—Choose, interpret, and talk with representations for fractions, decimals, and operations.
11. A fourth-grade teacher plans instruction to introduce ordering fractions on a number line. Which of the following activities would best prepare students for this concept?
- Students work in pairs on sorting fractions with unlike denominators from least to greatest value.
- Students view an engaging educational video that models the procedure for placing fractions on a number line.
- Students in a small group receive fractions from the teacher and then order themselves from least to greatest value.
- Students use benchmark numbers on a number line to support understanding of ordering fractions with like denominators.
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
- This activity is more appropriate for students to attempt after they understand how to order fractions using a number line.
- It would be more beneficial for student learning to show this video after students have had opportunities to develop a conceptual understanding of why the process works.
- This activity is more appropriate to do after the students have been introduced to the concept of ordering fractions on a number line.
- Correct. Of the activities shown, students are best prepared to order fractions if they have opportunities to use benchmark numbers (e.g., 1 half, 1 fourth) on a number line as a visual reference.
Objective 012—Elicit, interpret, support, and extend others' mathematical thinking for fractions, decimals, and operations.
12. A fourth-grade student states that 4 twelfths plus 6 twelfths = 10 twenty-fourths. Based on this statement, the teacher can most effectively use which of the following strategies to draw out the student's thinking and address misconceptions about computing with fractions?
- reviewing how to find common denominators and add fractions
- asking the student to model the addition problem by drawing a number line or using fraction blocks
- providing the student with additional problems involving fractions with like and unlike denominators
- using grids and other visual representations to model the relationship between numerators and denominators
- Answer. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
- This strategy does not provide a conceptual explanation of why denominators cannot be added.
- Correct. This strategy draws out the student’s thinking and provides an opportunity for them to observe why denominators cannot be added.
- This strategy does not provide any reteaching to address the student’s misconceptions about adding fractions.
- This strategy focuses on how to interpret a fraction, but it does not directly address why combining the two fractions leaves the denominator unchanged.